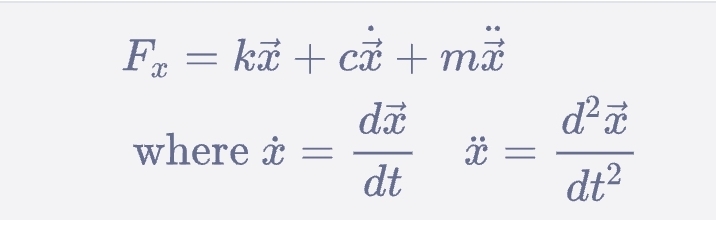
Fx: 沿x方向的力
x: 沿x方向的位移
x頂加一點: 沿x方向的位移速度
x頂加兩點: 沿x方向的位移加速度
k: 物質的剛度
c: 物質的阻尼系數
m: 物質的質量
t: 時間
帶箭咀的字母代表該變數為向量 (帶方向)
x: 沿x方向的位移
x頂加一點: 沿x方向的位移速度
x頂加兩點: 沿x方向的位移加速度
k: 物質的剛度
c: 物質的阻尼系數
m: 物質的質量
t: 時間
帶箭咀的字母代表該變數為向量 (帶方向)
沒有帶箭咀的字母代表該變數為標量 (不帶方向)
只看公式的右邊:
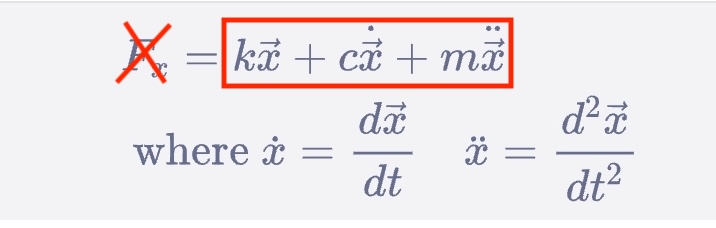
筆者必須一再重伸,我們只看這條力學公式的右邊,不要理會公式的左邊。
陳中華陳老師常說覺得自己有勁的人,總喜歡使勁。
筆者想大膽提出練習太極拳要先拼棄找力或找勁的想法,要是總以力或勁作為太極拳的拳藝高低的量度標準,那麼我們的思想框架就一直以發出大力大勁為我們拳藝的成就目標。常人都會有理想化自己的練習成績的傾向,所以想自己練了太極拳足夠長的時間,身上必定有太極勁,而且與日俱增,因而趨向認為自己很有勁,最終脫離不了喜歡使勁的困局。
陳老師在一個公開講座上談論 “落地生根”,他說人們一聽見”落地生根”都老幻想著自己的腿怎麼向地下生根,其實真正的”落地生根”只是如實執行拳裏的要求和步驟。
筆者認為,任何時候都應按陳老師的教導,以如實執行拳裏的要求和步驟為先,所以筆者強調只看公式的右邊,當我們只看公式的右邊,我們就會向怎樣實踐動作的長度和位移方向努力,追求打好每個動作,打好了每個動作之後,再研究用幾多時間去完成這個動作,再發展到我們要在什麼時機下做多快的動作。當我們練好動作和時間的掌控,我們想追求的太極勁就會間接結果。
班門弄斧
筆者的拳藝層級仍屬練習級別,要在各位拳友面前寫應用,實在是班門弄斧。不過筆者所識的這條力學公式,自覺其價值非凡,很想作出分享,無奈要說明它的價值,不得不從應用方面提供一些例子,以便拳友認識它的價值,所以筆者不得不紙上談兵一下介紹它,望各位包函。
林先生演示在筆者身上的勁
林先生一直強調身法和胯的定住活開,兩肩兩胯要練死使身像鐵板一樣,鬆沉一邊胯,開另一邊胯令身以鬆沉的那胯的垂直豎線為軸轉,身帶手公轉,由此基礎身法,將力由腳傳導到手上。每次林先生身一轉,透過他的手作用在筆者身上,筆者都感覺到像被一個巨大的球體撥開,完全站不住。
林先生有次再進階在筆者身上演示靠肘擠按旳轉換。林先生上步入身,肩靠筆者的身,然後一轉,由肩到肘到小臂的擠,最後到手的按,手的按並未有真正按下去,只是微微一碰,但筆者已知道,若這四法做全,筆者的屁屁必重挫在地上。而如何是四法做全?入身的靠以全速全身的質量撞過來,緊接全速身轉,帶肘和小臂各打一下並逼使筆者失去所有空間,最後手伸足下按,筆者旳屁屁就會應掌直坐地上。
我們現以這一條力學公式為觀察基準,分析這四法的演示,這四法包含了靠時步的速度 (dx/dt 或 v) , 靠時是全身的質量 (m), 肘和擠時是在進步的速度(dx/dt 或 v) 基礎下加一個旋轉的加速和轉向(d^2x/dt^2 或 a), 最後伸手按是長度 (x)。
旋轉與槓桿
陳老師簡單定義了兩頭和中間,即一支棍的兩端盡頭和正中間的中點。這三點可以任意設定其中一點為不動點,整支棍以該點為支點旋轉。以下以圖展視這三類旋轉。
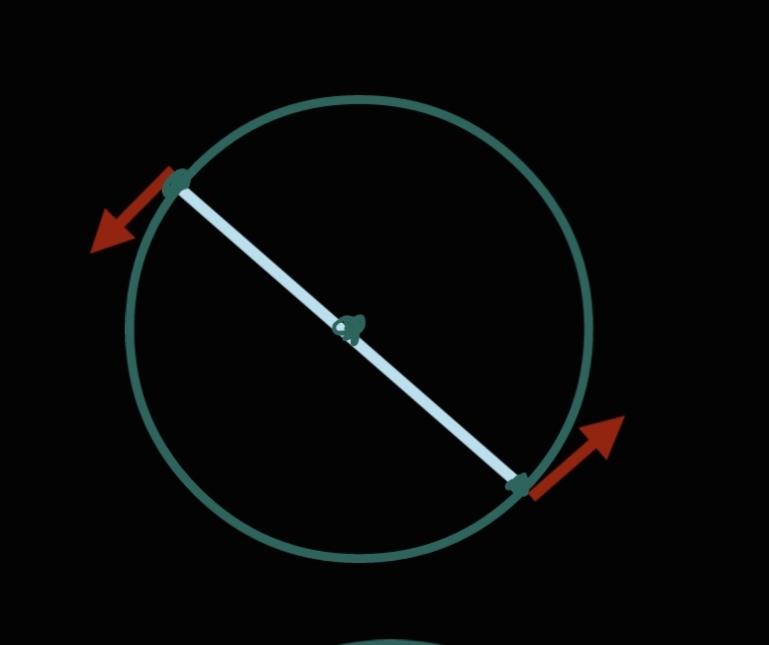
上圖為第一類以中心(通常是丹田或胯)為支點旋轉
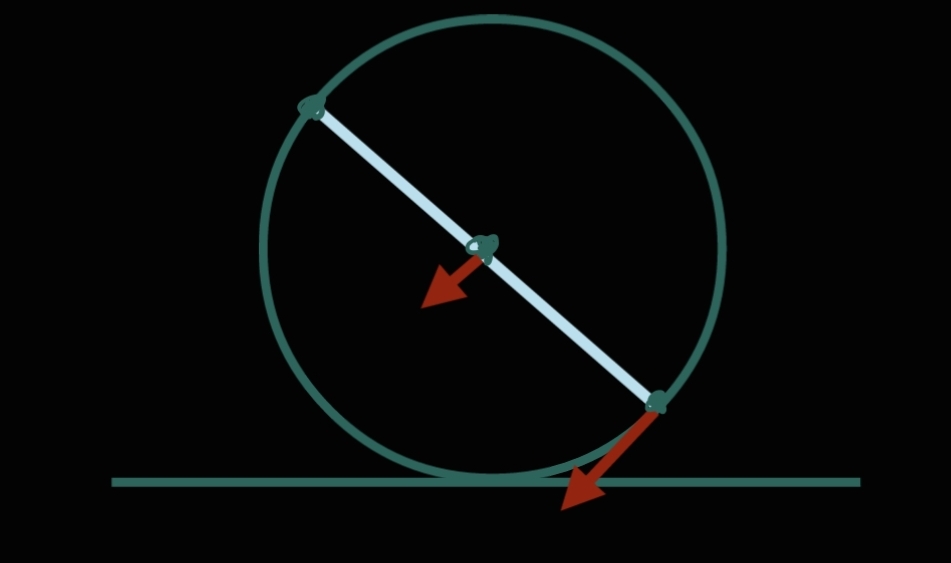
上圖為第二類以接觸點(通常是手)為支點旋轉
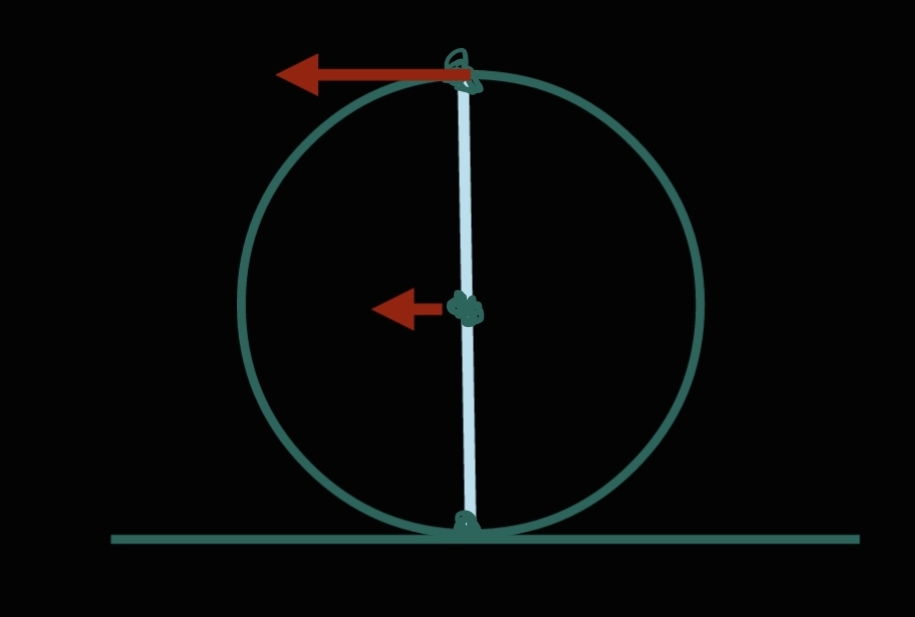
上圖為第三類以根節(通常是腳和肩)為支點旋轉
第一類旋轉包括:
- 定步轉胯或者轉丹田。
- 定前腳,後腳開步,手往開步的相反方向公轉。
上段林先生演示的四法轉換是屬第二類旋轉接第一類旋轉再接第三類旋轉。林先生進步肩靠是第二類旋轉,然後肘擠是第一類旋轉,伸手按是第三類旋轉。
旋轉除了不動的支點,其餘的兩點都有位移,我們可以以這兩點的其中一點為旋轉的發動點,這一條力學公式的 x 就可用以描述這發動點的位移,控制這位移x 的長短,就是控制旋轉的幅度。然後我們控制用多少時間完成這個x的位移,就控制公式中的 dx/dt 和 d^2x/dt^2 。
透過選取支點,發動點和被作用點,就生成相應的力臂重臂長度比例,發揮相應的省力槓桿,費力槓桿和等臂槓桿作用。
在這一條力學公式裏的x通常被用作描述位移,但它亦俱有長度的意思,所以也可以幫助我們緊記力臂重臂比例的重要性,而非一味想著直接在接觸點上用多少力。
目標
陳老師總結太極的勁是間接力,無論前文”圓內三角”所述的伸撥勁的直橫轉換,或是上段旋轉與槓桿,都是間接力,發動點的位移產生間接作用在接觸點上。這種間接操作對常人來說並不直觀,所以我們學習實用拳法的動作,往往只能顧著做動作,忘了要兼顧打中目標。做了動作,但沒有打中目標,技巧就不起作用。
對方的中就是我們的目標,中包括幾何的中,和質量的中。沿著整條脊椎都是幾何的中,質量的中有頭和丹田。
筆者提出這一條力學公式,當中包含的向量,就是提醒我們的作用方向必要擊中目標。
向量
根據數學,我們知道一支向量可以由複數的向量分量組成。
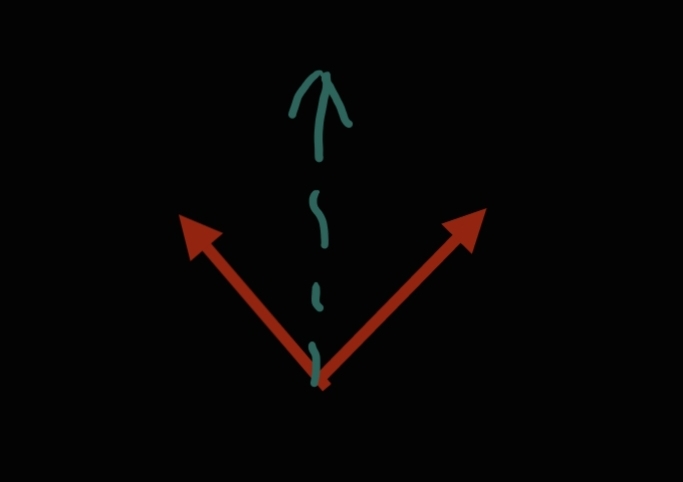
上圖裏,綠色虚線箭咀代表向量,紅色實線箭咀代表綠色虛線箭咀的向量分量。我們並非直接執行虚線向量,我們只同時直接執行實線向量,以達到相當於虚線向量的效果。
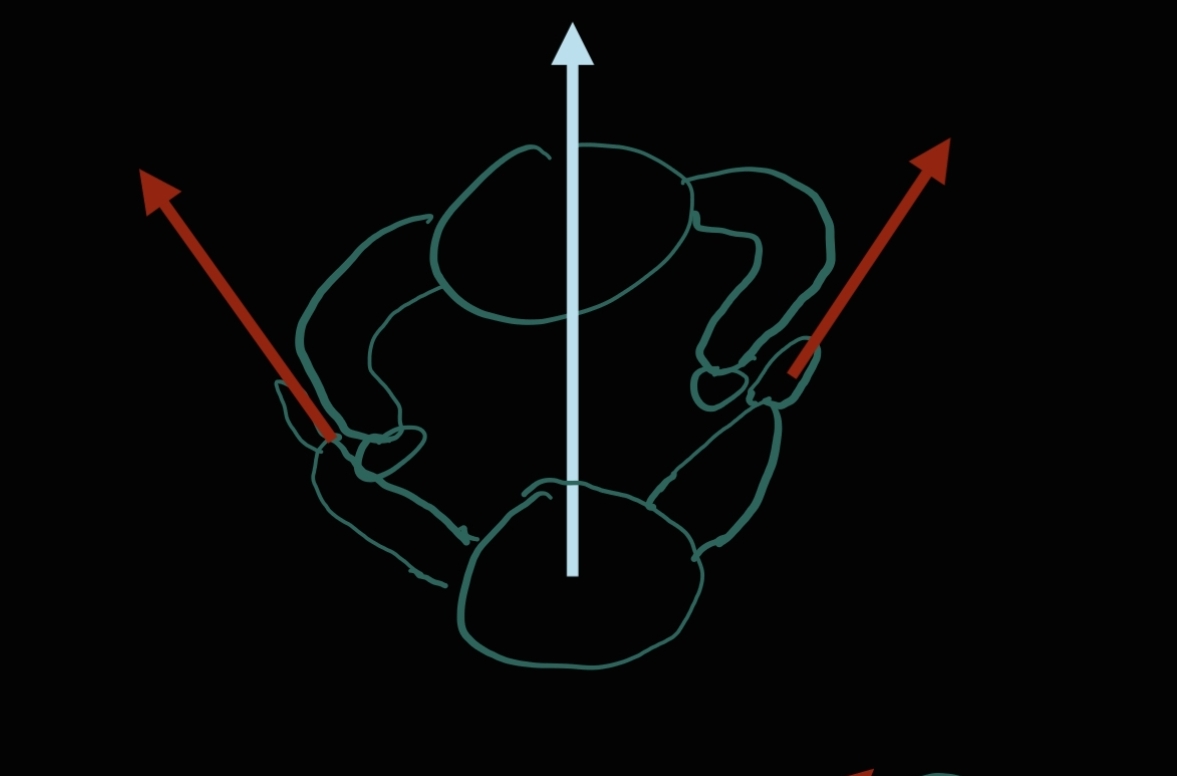
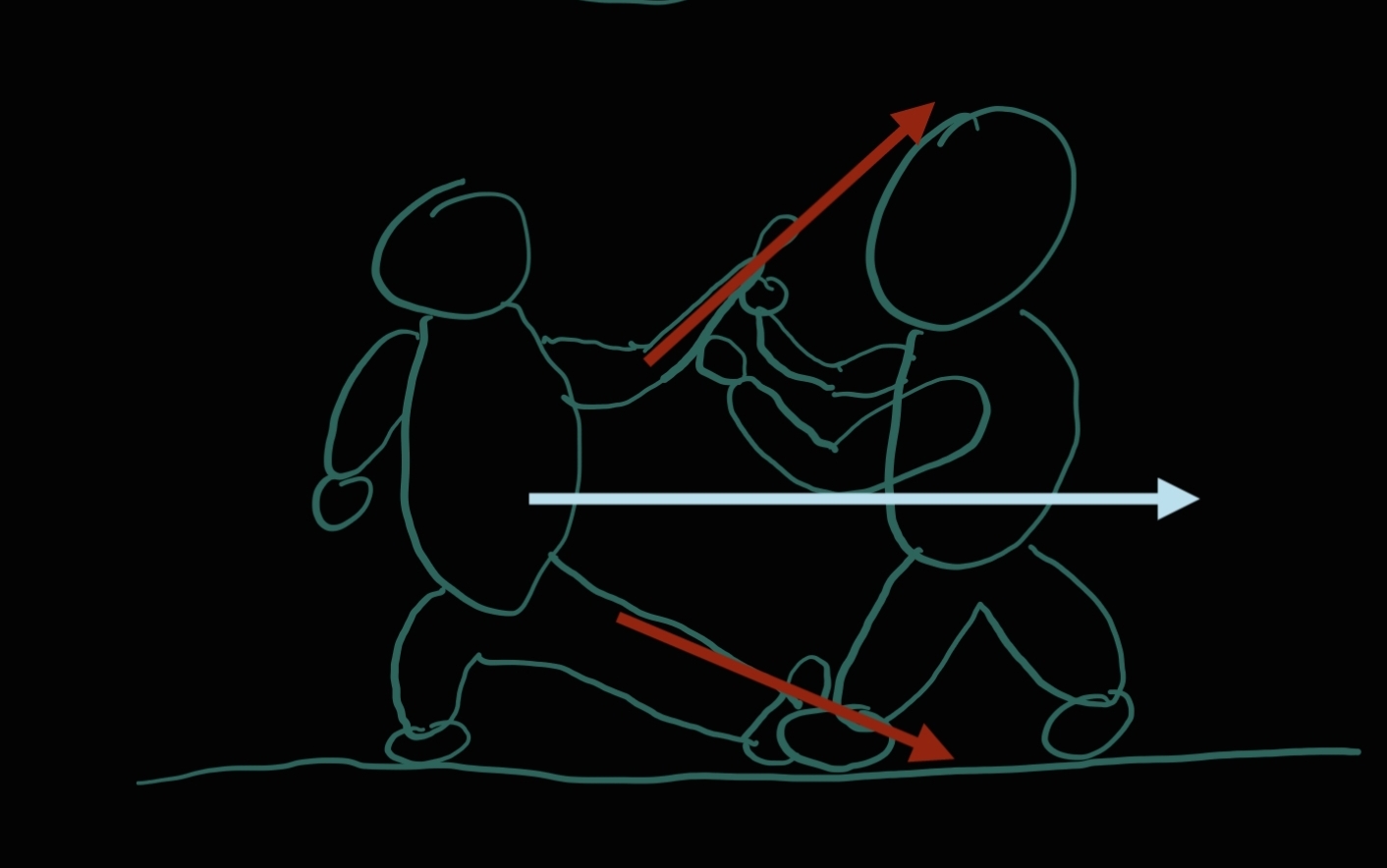
公式裏的x在這個兩個情況可以用來描述手和腿的位移,而應用效果的輸出則是以這位移的長度(x),速度 (dx/dt 或 v)和加速度控制 (d^2x/dt^2 或 a)。
不可控和半可控的k,c,m
k是剛度,c是阻尼系數,m是質量。
這3個變數可被分成兩組,一組代表自己的 k(我), c(我), m(我), 另一組代表對方的 k(對方), c(對方), m(對方)。
k(對方), c(對方), m(對方) 代表對方的肌肉和骨的剛度,他的關節轉動能力,他的重量,這些基本都是不可控的。m(對方)可以憑肉眼判斷,k(對方)和c(對方)一般是不能看見的,要去碰他的身體,憑經驗量度他。
如前文 “一條力學公式 – 2.練習篇” 裏的 “A4) 林先生給筆者蓄彈簧勁” 段所述,如發現對方是一個彈性皮球,我們可多利用他的反彈特性控制他的重心。
k(我), m(我)在應用時都是半可控的。
陳老師說金剛倒錐接手,我們的手必定要硬,讓對方吃痛,這個硬,是透過實時改變肌肉剛度k(我)達成。臨陣時,我們肌肉的剛度狀態k(我)是可以改變的,不過我們肌肉的剛度k(我)最大/最小值和我們肌肉剛度變化的速度完全取決於練習。
掩手肱捶打出的拳,我們可以分3個程度使出:
m(我)在應用時是有局部身體體重 “有效m(我)” 和 我們整個體重“總m(我)” 之分。“有效m(我)”是計算動的身體部分的m(我),如手,身,腿。實用拳法追求不動,較少運用全身一起移動高速衝擊對方,所以運用動量的機會比較小。實用拳法講求分陰陽,身和手分開,左右分開,上下分開,執行身體局部獨立動作比較多,所以“有效m(我)” 相對“總m(我)”比較重要。臨陣時,我們可以按我們分陰陽的能力控制“有效m(我)”以調節掩手肱捶的輸出大小,但無法改變自己分陰陽的能力,分陰陽的能力完全來自於練習。
c(我)在應用時是不可控的。我們的關節活動能力完全由我們的練習決定,臨陣時已無法改變。
x, dx/dt, d^2x/dt^2
筆者認為在應用時,k, c, m是相對次要的。我們應該注意 x, dx/dt 或 v, d^2x/dt^2 或 a。
而 dx/dt, d^2x/dt^2 這兩個變數其實是由位移 x 衍生出來,我們先設定位移 x。我們將自己的手由對方身前的位置伸到對方身後的位置,這兩個位置的距離就是 x。然後我們設定我們用多少時間去完成這個位移,dx/dt, d^2x/dt^2 就被衍生出來。所以我們再可將這3個變數 (x, dx/dt, d^2x/dt^2)再簡化成2個:位移x 和 時間t 。
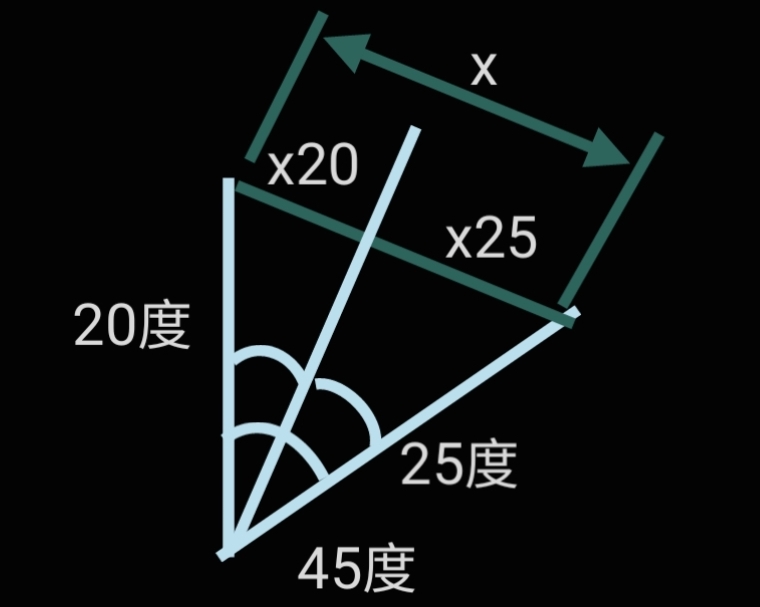
以金剛倒錐接手右轉身45度為例,我們右轉身會帶動我們的手位移x。我們將這45度轉身分成 20度和 25度兩個部分,前20度轉身手的位移是 x20 ,後25度轉身手的位移是 x25 。 所以 x = x20 + x25 。我們用一個長時間去完成位移x20 (相當於一路緩慢而均勻的速度), 緊接用一個極短時間去完成剩下來的位移x25 (相當於二路急速的速度)。這樣我們在頭20度轉身會在對方手上產生 “捋”,後25度轉身在對方手上產生 “採”,”挒”或”採+挒” (視乎我們雙手在變速過程中做出怎樣的變向)。
結語
很多太極的家派主張講 “氣”和”鬆”,從學者通常都依憑自己的主觀感覺去判斷自己有沒有做到這兩個字,無論關節能不能圓轉自如的人,老師叫他放鬆,他放鬆,然後都會自覺很鬆。
“力”和”勁”都帶有這種主觀感覺的味道,關節能不能圓轉自如的人都可以在練拳過程中感到自己很有勁。
但關節不能圓轉自如的人是不能如實執行拳式動作和要求。所以筆者提出這一條力學公式,以位移作為我們客觀量度自己拳藝的標準,以由位移和時間作基礎衍生的速度和加速度作為控制輸出的參數。
降低互相試練時無心傷害同門的風險,提高量度自己實用拳法造藝的準確度。
更多帖子
- 一條力學公式 - 1.導讀篇 (强烈推荐)
- 一條力學公式 - 2.練習篇 (强烈推荐)
 :18963387833
:18963387833